happy coding
[lecture] BASIC CONCEPTS 본문
Algorithm specification
알고리즘은 유한한 일련의 명령을 해결하는 것이다. 알고리즘의 조건에는 1. 0개 이상의 입력 2. 적어도 1개의 출력 3. 모호하지 않은 명확성 4. 한정된 수의 단계 후에 종료되는 유한성 5. 프로그램과는 다른 ??? 이 있다.
//Binary Search
assumption
sorted n (>=1) distinct integers
stored in the array list
return
index i (if i, list[i] = searchnum)
or -1 (otherwise)
denote left and right
left and right ends of the list to be searched
initially, left = 0 and right = n-1
let middle = (left + right) / 2
middle position in the list
compare list[middle] with the searchnum and adjust left or right
1. searchnum < list[middle]
set right to middle -1
2. searchnum = list[middle]
return middle
3. searchnum > list[middle]
set left to middle + 1
if searchnum has not been found and there are more integers to check
recalculate middle and continue searchwhile(there are more integers to check){
middle = (left + right) / 2;
if(searchnum < list[middle])
right = middle - 1;
else if(searchnum == list[middle])
return middle;
else
left = middle + 1;
}
//binary search
int bindsearch(int list[], int searchnum, int left, int right){
int middle;
while(left <= right){
middle = (left + right) / 2;
switch(COMPARE(list[middle], searchnum)){
case -1 : left = middle + 1;
break;
case 0 : return middle;
case 1 : right = middle - 1;
}
}
return -1;
}Recursive Algorithms
direct recursion - call themselves
indirect recursion - call other function that invoke the calling function again
recursive mechanism - extremely powerful, allows us to express a complex process in very clear terms
any function that we can write using assignment, if-else, and while statements can be written recursively
//binary search
/*transform iterative version of a binary search into a recursive one
establish boundary condition that terminate the recursive call
1. success > list[middle] = searchnum
2. failure > left & right indices cross
implement the recursive calls so that each call brings us one step closer to a solution*/
int binsearch(int list[], int searchnum, int left, int right){
int middle;
if(left <= right){
middle = (left + right) / 2;
switch(COMPARE(list[middle], searchnum)){
case -1 : return
binsearch(list, searchnum, middle + 1, right);
case 0 : return middle
case 1 : return
binsearch(list, searchnum, left, middle - 1);
}
}
return -1;
}Performance Analysis
performance evaluation 1. performance analysis : machine independent, complexity theory 2. performance measurement : machine dependent
space complexity : the amount of memory that it needs to run to completion
time complexity : the amount of computer time that it needs to run to completion
space complexity
fixed space requirements : don't depend on the number and size of the program's inputs and outputs, eg) instruction space, simple variables, fixed-size structured variables, constants
variable space requirement : the space needed by structured variable whose size depends on the particular instance, I, of the problem being solved
total space requirement S(P) : S(P) = c + SP(I)
c : constant representing the fixed space requirements
SP(I) : function of some characteristics of the instance I
float abc(float a, float b, float c){
return a+b+b*c+(a+b-c)/(a+b)+4.00;
}
/*
input - three simple variables
output - a simple variable
fixed space requirements only Sabc(I) = 0
*///Iterative version
float sum(float list[], int n){
float tempsum = 0;
int i;
for(i=0; i<n; i++)
tempsum += list[i];
return tempsum;
}
/*
output - a simple variable
input - an array variable
*/Pascal pass arrays by value : entire array is copied into temporary storage before the function is executed
Ssum(I) = Ssum(n) = n
C pass arrays by pointer : passing the address of the first element of the array
Ssum(n) = 0
//Recursive version
float rsum(float list[], int n){
if(n) return rsum(list,n-1) + list[n-1];
return 0;
}handled resursively : compiler must save 1. the parameters 2. the local variables 3. the return address, for each recursive call
space needed for one recursive call : number of bytes required for the two parameters and the return address
6 bytes needed on 80386 > 2 bytes for pointer list[], 2 bytes for integer n, 2 bytes for return address
assume array has n = MAX_SIZE numbers >> total variable space Srsum(MAX_SIZE) : Srsum(MAX_SIZE) = 6 * MAX_SIZE
Time complexity
The time T(P), taken by a program P, is the sum of its compile time and its run(or execution) time > we really concerned only with the program's execution time, Tp
count the number of operations the program perform > give a machine-independent estimation
program step : a syntatically or semantically meaningful program segment whose execution time is independent of the iinstance characteristics
tabular method : construct a step count table 1. first determine the step count for each statement(steps/execution) 2. next figure out the number of times that each statement is executed(frequency) 3. total steps for each statement (total steps) = (s/e) * (frequency)


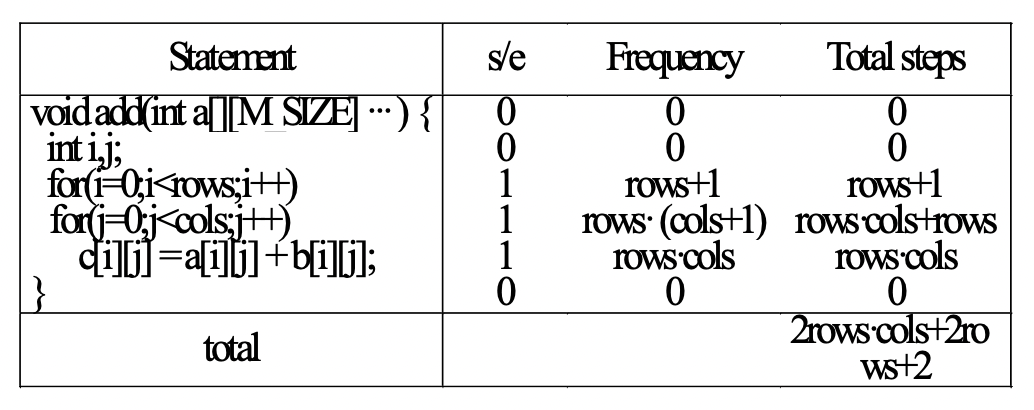
time complexity factors
input size : depends on size of input(n) => T(n) = ?
input form
- depends on different possible input formats 1. avarage case : A(n) ? 2. worst case : W(n) = ?
- concerns mostly for "worst case"
- worst case gives "upper bound"
comparing time complexities
- exist different algorithms for the same task
Asymptotic Notation(점근적 표기법)
Big "OH" : f(n) = O(g(n)), iff there exist positive constants c and n0 such that f(n) <= c*g(n) for all n, n>= n0
ex) f(n) = 25*n, g(n) = 1/3*n2 >> 25*n = O(n2/3) if let c = 1 >> |25*n| <= 1*|n2/3| for all n>= 75
g(n) is an upper bound on the value of f(n) for all n, n >= n0. but, doesn't say anything about how good this bound is n = O(n2)... g(n) should be as small a function of n as one can come up with for which f(n) = O(g(n))

Omega : f(n) = Ω(g(n)), iff there exist positive constants c and n0such that f(n) >= c*g(n) for all n, n>= n0
g(n) is a lower bound on the value of f(n) for all n, n >= n0. should be as large a function of n as possible
theorem) if f(n) = amnm + .. + a1n + a0 and am>0, then f(n) = Ω(nm)
Theta : f(n) = θ(g(n)), iff there exist positive constants, c1, c2, and n0 such that c1*g(n) <= f(n) <= c2*g(n) for all n, n>= n0
more precise than both the "big Oh" and omega notations, g(n) is both an upper and lower bound on f(n)
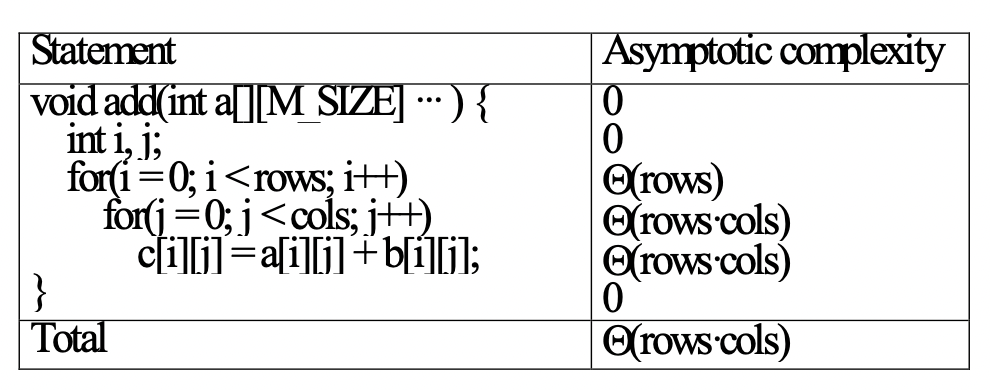

polynomial time : tractable problem
exponential time : intractable (hard) problem
eg) sequential search, binary search, insertion sort, heap sort, satisfiablity problem, testing serializable scheduling
'lecture > data structure' 카테고리의 다른 글
| [lecture] Heap (0) | 2023.01.10 |
|---|---|
| [lecture] 그래프 (0) | 2023.01.09 |
| [lecture] 트리 (0) | 2023.01.09 |
| [lecture] 큐 (0) | 2023.01.09 |
| [lecture] 스택 (0) | 2023.01.01 |




