happy coding
[lecture] 스택 본문
스택(stack)
논리적 개념으로는 linear list(ordered list) 에서 array와 linked list 가 있다. 이를 통해 stack 또는 queue를 구현한다.
연결리스트는 동적인 자료구조, 순차 접근 방식, O(n), 데이터의 접근과 탐색이 중요할 때 사용한다.
배열은 정적인 자료구조, 임의 접근 방식, O(1), 데이터의 추가와 삭제가 중요할 때 사용한다.
스택은 삽입과 삭제는 O(1)이고, 탐색은 O(n)이다. 큐 또한 같다.
스택이란, 접시를 쌓듯이 같은 크기의 자료를 차곡차곡 쌓아 올린 형태의 자료구조를 말한다. 스택에 저장된 원소는 top으로 정한 곳에서만 접근이 가능하다. 여기서, top의 위치에서만 원소를 삽입하므로 먼저 삽입한 원소(가장 최근에 들어온 데이터)는 밑에 쌓이고, 나중에 삽입한 원소는 위에 쌓인다. 이는 LIFO(Last-In-First-Out)을 의미한다. > 중간에 넣을 수 없다.
스택에서의 삽입 연산을 push, 삭제 연산을 pop이라고 한다.
| Boolean empty() | stack이 비어있는지 확인하는 함수 |
| peek() | stack의 최상단 데이터를 삭제하지 않고 해당 데이터 반환하는 함수 |
| pop() | stack의 최상단 데이터를 삭제하고 해당 데이터를 반환하는 함수 |
| push(E item) | stack의 최상단 부분에 데이터를 입력하는 함수 |
| int search(Object o) | stack의 최상단에서부터 찾고자 하는 데이터가 몇 번째에 존재하는지 반환 |
- stack underflow : 비어 있는 스택에 pop()을 해 top의 값이 0보다 작아지는 경우 > 꺼낼 수 없는 상태
- stack overflow : 꽉 차있는 스택에 push()를 하여 스택의 최대 용량을 벗어나는 경우 > 더 이상 입력할 수 없는 상태
Stack Abstract Data Type
LIFO을 가짐. 데이터 타입을 추상화 시키는 것 = 개념과 사용법만 표현한 것

시스템 스택
return address를 스택에 담고, local variables 까지 stack frame이 되어, pop될 때는 frame 단위로 삭제된다.

stack frame(activation record)은 function call을 하는 경우 자동으로 생성된다.
함수의 실행이 끝나면 자신을 호출한 함수로 되돌아감. 이 때 스택은 복귀할 주소를 기억하는 데 사용된다. 함수는 호출된 역순으로 되돌아가야 하기 때문이다. 시스템 스택에는 함수가 호출될 때마다 활성 레코드가 만들어지며, 이 곳에 복귀 주소가 저장된다. 활성 레코드에 생성되는 정보는 1. 복귀 주소 2. 프로그램 카운터 3. 매개변수 4. 함수 안에서 선언된 지역변수 이다.



//IsEmpty(stack)
return (top < 0);
//IsFull(stack)
return (top >= MAX_STACK_SIZE - 1);
//Push(stack, item)
void push(int *ptop, element item){
if(*ptop >= MAX_STACK_SIZE - 1){
stack_full();
return;
}
stack[++*ptop] = item;
}
//pop(stack)
element pop(int *ptop){
if(*ptop == -1)
return stack_empty();
return stack[(*ptop)--];
}element stack[MAX_STACK_SIZE];
int top = -1;
main(){
item = ..;
push(&top,item); //push 하나 성공!
}A Mazing Problem :: 스택 응용
미로를 자료구조로 표현하는 방법 : 스택
mark array pop push
Evaluation of Expressions :: 스택 응용
스택을 이용한 계산기 1. infix form : opnd (optr) opnd 2. postfix form : opnd opnd (optr)
컴파일러는 stack을 사용해서 1. translation 2. evaluation 한다. (two pass)

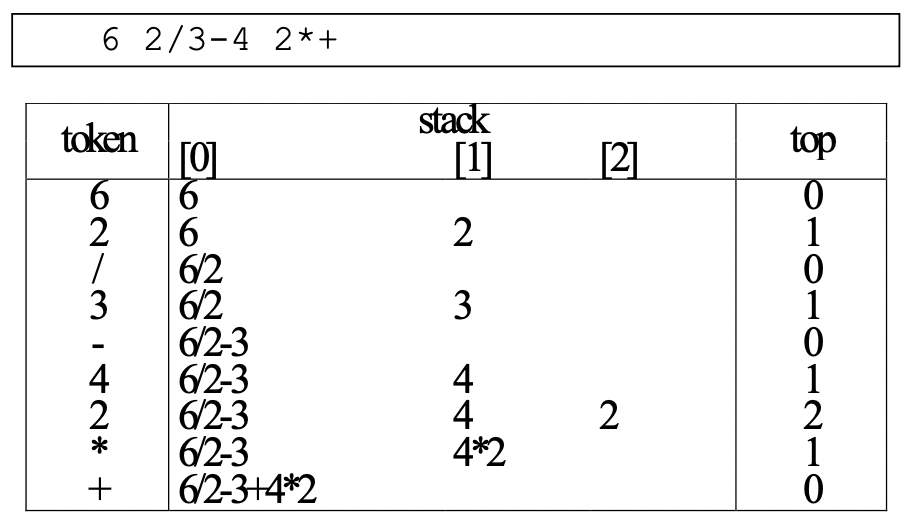
| get_token() | used to obtain tokens from the expression string | |
| eval() | token 이 operand 인 경우, convert it to number and push to the stack | otherwise, stack에서 연산자 2개 pop > perform the specified operation > 스택에 결과 push |
operand는 push해 저장, operand가 아니면 stack에서 2개를 뽑아, 먼저가 right operand, 다음이 left operand. 계산을 해서 결과를 stack에 저장한 후 다음 처리하기.
int eval(){
precedence token;
char symbol;
int op1, op2;
int n=0;
int top = -1;
token = get_token(&symbol, &n);
while(token != eos)
if(token == operand)
push(&top, symbol - '0');
else{
op2 = pop(&top);
op1 = pop(&top);
switch(token){
case plus : push(&top, op1 + op2); break;
case minus : push(&top, op1 - op2); break;
case times : push(&top, op1 * op2); break;
case divide : push(&top, op1 / op2); break;
cas mod : push(&top, op1 % op2);
}
}token = get_token(&symbol, &n); //next token
}return pop(&top);시간 복잡도 : O(n), n은 number of symbols in expression, 공간 복잡도 : stack[MAX_STACK_SIZE] + expr[MAX_STACK_SIZE]
Infix to Postfix
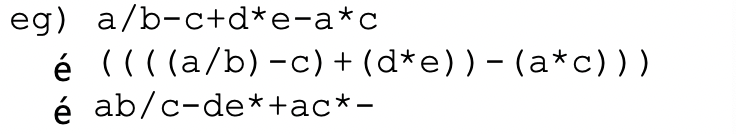
1. 표현을 완전히 괄호로 묶다
2. 모든 이진 연산자를 이동하여 해당 오른쪽 괄호를 바꿉니다
3. 괄호를 모두 삭제
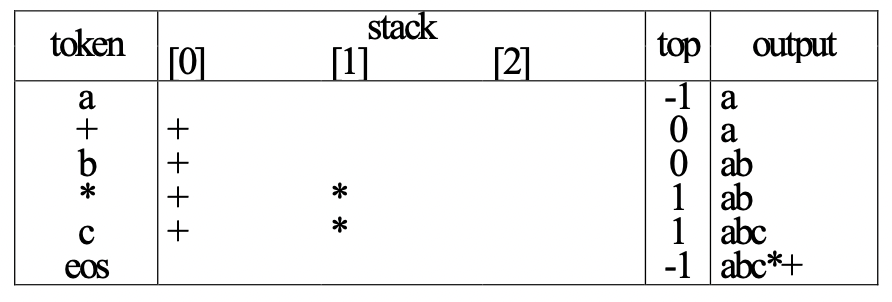
괄호가 있는 경우(postfix에는 괄호가 없다) : 오른쪽 괄호 토큰을 만난 경우, 왼쪽 괄호를 pop할 때까지 stack에서 pop한 후, 괄호를 모두 삭제한다.
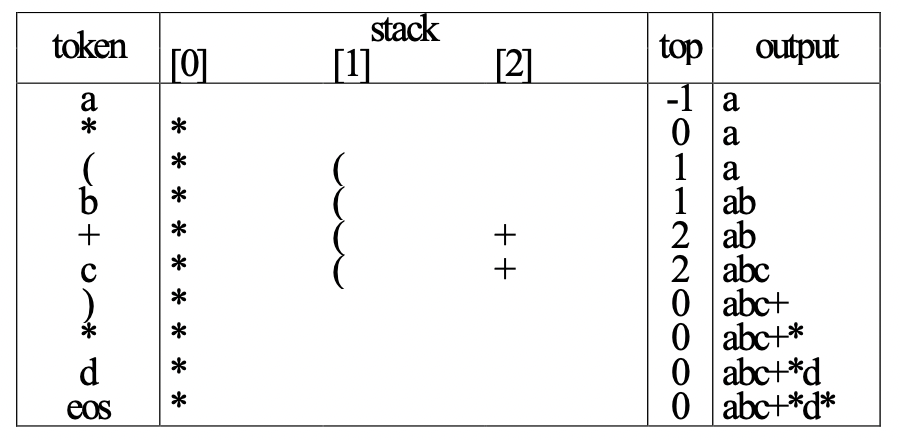
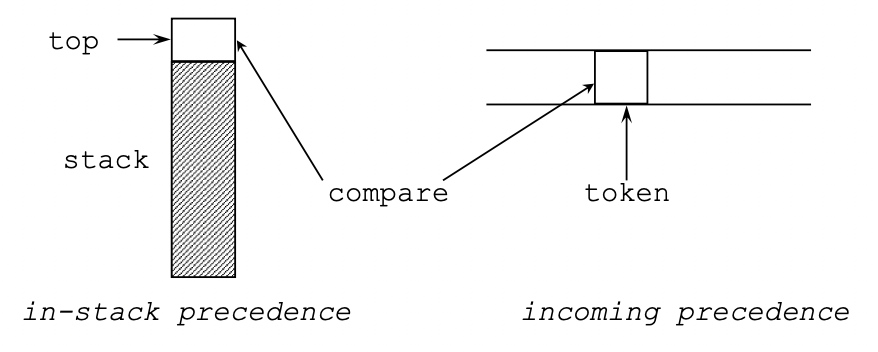
top과 token의 우선순위
isp(in-stack precedence) < icp(incoming precedence) 라면 push
isp > icp 라면 pop and print
(왼쪽 괄호 때문에 우선순위를 다르게 표시해야 한다.) incoming에서 문자열 사이에 있는 경우 무조건 push되려면 제일 높은 우선순위(나오기 전엔 가장 높은 우선순위)를 가져야 하나, in-stack에서는 제일 낮아야 나올 수 있다. 따라서 stack[0] eos;
void postfix(void){
char symbol;
precedence token;
int n = 0;
int top = 0;
stack[0] = eos;
for (token = get_token(&symbol, &n); token != eos; token = get_token(&symbol, &n)){
if (token == operand) // + - * /
printf("%c", symbol);
else if (token == rparen){
while(stack[top] != lparen) //왼쪽 괄호 나올 때까지 pop한다.
print_token(pop(&top));
pop(&top); //(을 pop해서 버린다.
}
else{
while(isp[stack[top]] >= icp[token]) //우선순위 따져서 pop한다.
print_token(pop(&top));
push(&top, token);
}
}
while((token = pop(&top)) != eos)
print_token(token);
printf("\n");
}postfix는 parenthesis, precedence가 필요없다. 시간 복잡도는 O(r), r은 number of symbols in expression. 공간 복잡도는 S(n) = n, n은 number of operators. 여기서 r = n + m ( m은 opnd 개수 )
'lecture > data structure' 카테고리의 다른 글
| [lecture] 트리 (0) | 2023.01.09 |
|---|---|
| [lecture] 큐 (0) | 2023.01.09 |
| [lecture] 연결 자료구조 (0) | 2022.12.30 |
| [lecture] C언어복습.연결리스트 (0) | 2022.12.29 |
| [lecture] C언어복습.동적메모리 (0) | 2022.12.29 |


