happy coding
[lecture] 트리 본문
트리
트리(Tree)란 계층적인 구조를 나타내는 자료구조를 의미하고, 부모-자식 관계의 1개 이상의 노드들로 이루어진다. 서브트리와 루트노드가 있다. 사이클이 없는 그래프,
노드(node) : 트리의 구성요소
루트(root) : 부모가 없는 노드
서브트리(subtree) : 하나의 노드와 그 노드들의 자손들로 이루어진 트리
단말 노드(terminal node) : 자식이 없는 노드
비단말 노드(nonterminal node) : 적어도 하나의 자식을 가지는 노드
레벨(level) : 트리의 각 층의 번호
높이(height) : 트리의 최대 레벨
차수(degree) : 노드가 가지고 있는 자식 노드의 개수
이진 트리
이진 트리(binary tree)는 모든 노드가 2개의 서브 트리를 가지고 있는 트리이며 공집합일 수도 있다 최대 2개까지의 자식 노드가 존재하며, 모든 노드의 차수가 2 이하이기 때문에 구현하기가 편리하다. 이진 트리에는 서브 트리간의 순서가 존재한다.
이진 트리에서 노드의 개수가 n개일 때 간선의 개수는 n-1이다. 높이가 h인 이진 트리인 경우, 최소 h개의 노드를 가지며 최대 2h-1개의 노드를 가진다. 여기서 높이는 최대 n이거나 최소 log2(n+1)이다. 여기서 n2 + n1 + n0 = 2n2 + n1 + 1 >> n0 = n2 + 1

| 포화 이진 트리(full binary tree) | 트리의 각 레벨에 노드가 꽉 차있는 이진 트리 |
| 완전 이진 트리(complete binary tree) | 높이가 h일 때, 레벨 1부터 h까지는 노드가 모두 채워져 있고 마지막 레벨 h에서는 왼쪽부터 오른쪽까지 노드가 순서대로 채워져 있는 이진 트리 |
| 사향 트리(Skewed binary tree) | 한쪽으로 기울어진 트리, 편향 트리라고도 부름 |
| 스레드 이진 트리(thread binary tree) | 노드의 링크가 null인 부분을 트리 운행에 사용하는 이진 트리, 왼쪽 링크가 Null인 경우 이전 노드의 위치를 기억, 오른쪽 링크가 null인 경우 이후 노드의 위치를 기억 |
이진 트리를 표현하는 방법에는 1. 배열표현법 2. 링크표현법 이 있다.
| 배열 표현법 | 모든 이진 트리를 포화 이진 트리라고 가정하고 각 노드에 번호를 붙여 그 번호를 배열의 인덱스로 삼아 노드의 데이터를 배열에 저장하는 방법 (a)의 완전 이진 트리인 경우, 좌우로 방향을 잡아 0번을 비워두고 순서대로 배열에 저장하는 것으로 빈공간이 없다. (b)의 shewed binary tree인 경우는 array에서 빈공간이 많이 생기기 때문에 효율이 떨어진다. |
 |
| 링크 표현법 | 포인터를 이용하여 부모노드가 자식노드를 가리키게 하는 방법 (child로 가는 것(edge)을 모두 link로 나타내고 더이상 child가 없는 null의 경우, link 또한 null로 저장한다. shewed binary tree인 경우, single linked list와 유사하다. |
 |
이진 트리의 순회
순회(traversal)란 트리의 노드들을 체계적으로 1번씩 방문하는 것을 의미하는데 여기에는 1. 전위 순회 2. 중위 순회 3. 후위 순회 가 있다.
| 전위 순회(preorder traversal) | VLR : 자손 노드보다 루트 노드를 먼저 방문한다. | + * a b / c d : prefix 응용 : 목차 만들기, 구조화된 문서 출력 |
 |
| 중위 순회(inorder traversal) | LVR : 왼쪽 자손, 루트, 오른쪽 자손 순으로 방문한다. | a * b + c / d : inorder fix |
 |
| 후위 순회(postorder traversal) | LRV : 루트 노드보다 자손을 먼저 방문한다. | a b * c d / + : post fix 응용 : 디렉토리 용량 계산 |
 |
트리에 엑세스하는 경우 루트부터 시작해야 하며, 루트 노드에 대한 인덱스(포인터)를 가지고 있어야 한다.
루트가 null일 때까지 내려간 후 return
후위 순회에서는 a[0, ... ,n] = a[0, ...,n-1] + a[n] 이라는 recurrence relation 이 있어야 한다.
//전위 순회
preorder(TreeNode *root){
if(root){
printf("%d", root->data); //노드 방문
preorder(root->left); //왼쪽 서브 트리 순회
preorder(root->right); //오른쪽 서브 트리 순회
}
}
//중위 순회
inorder(TreeNode *root){
if(root){
inorder(root->left); //왼쪽 서브 트리 순회
printf("%d", root->data); //노드 방문
inorder(root->right); //오른쪽 서브 트리 순회
}
}
//후위 순회
postorder(TreeNode *root){
if(root){
postorder(root->left); //왼쪽 서브 트리 순회
postorder(root->right); //오른쪽 서브 트리 순회
printf("%d", root->data); //노드 방문
}
}void preorder(tree_ptr ptr){
if(ptr){
printf("%d", ptr->data);
preorder(ptr->left_child);
preorder(ptr->right_child);
}
}
void inorder(tree_ptr ptr){
if(ptr){
inorder(ptr -> left_child);
printf("%d", ptr->data);
inorder(ptr->right_child);
}
}
void postorder(tree_ptr ptr){
if(ptr){
postorder(ptr->left_child);
postorder(ptr->right_child);
printf("%d",ptr->data);
}
}이진 트리 순회의 시간복잡도는 O(n), n은 트리 내의 노드 수. 공간 복잡도는 stacksize 에 O(n), n은 트리의 최악의 depth(case of skewed binary tree)
lterative inorder traversal
| pros : 단순하고 간결한 표현, 좋은 가독성, 구현 세부 정보를 알 필요 없음 |
| cons : 대용량 저장소 필요, 실행 속도 느림 |
//iterative inorder traversal, 루프로 구현하기
void iter_inorder(tree_ptr node){
int top = -1;
tree_ptr stack[MAX_STACK_SIZE];
while (1){
while(node){
push(&top, node);
node = node->left_child;
}
node = pop(&top);
if(!node) break; //NULL이면 break
printf("%d", node->data);
node = node->right_child;
}
}preorder, inorder, postorder >> stack 이용, level order >> queue 이용
Lever order traversal
형제 노드 간 링크가 없는 경우, 2->3으로 가야 하는 데, queue 를 사용한다.
//level order traversal
void level_order(tree_ptr ptr){ //root에서 출발
int front = rear = 0;
tree_ptr queue[MAX_QUEUE_SIZE];
if(!ptr) return; //ptr == NULL인 경우
addq(front, &rear, ptr);
while(1){
ptr = deleteq(&front, rear); //root를 queue에서 빼기
if(ptr){
printf("%d", ptr->data);
if(ptr->left_child)
addq(front, &rear, ptr->left_child);
if(ptr->right_child)
addq(front, &rear, ptr->right_child);
}
else break;
}
}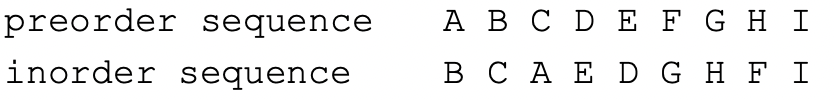
copying binary tree
//copying binary trees
tree_ptr copy(tree_ptr original){
tree_ptr temp;
if(original){
temp = (tree_ptr)malloc(sizeof(node));
if(IS_FULL(temp)) exit(1);
temp->left_child = //child 부분 먼저 copy
copy(original->left_child);
temp->right_child =
copy(original->right_child);
temp->data = original->data; //data copy
return temp; //root temp copy
}
return NULL;
}testing for equality of binary trees
//testing for equality of binary trees
int equal(tree_ptr firt, tree_ptr second){
return ((!first && !second) || //둘다 null
(first && second //또는
&& (first->data == second->data)
&& equal(first->left_child, second->left_child)
&& equal(first->right_child, second->right_child));
}이진 탐색 트리(binary search tree, BST)
이진 탐색 트리란 중복안되는 키 값을 가지며, 탐색 작업을 효율적으로 하기 위한 (index용) 자료구조이다. key(왼쪽 서브 트리) <= key(루트 노드) <= key(오른쪽 서브 트리) 이며, 이진 탐색을 중위 순회하면 오름차순으로 정렬된 값을 얻을 수 있다. 루트를 기준으로 루트보다 작은 값은 왼쪽 서브 트리에, 루트보다 큰 값이면 오른쪽 서브 트리로 위치 시키게 한다. 탐색작업을 하는 경우 원소의 개수가 n일 때, 시간 복잡도는 O(log2n)이다.
이 탐색 작업에서 array로 하는 경우 원소의 개수가 n일 때 시간복잡도는 O(n)이다.
이진 탐색 트리에서의 탐색 연산에서
- 비교한 결과가 같으면 탐색이 성공적으로 끝나게 된다.
- 주어진 키 값이 루트 노드의 키 값보다 작으면 탐색은 이 루트 노드의 왼쪽 자식을 기준으로 다시 시작한다.
- 주어진 키 값이 루트 노드의 키 값보다 크면 탐색은 이 루트 노드의 오른쪽 자식을 기준으로 다시 시작한다.
search(x,k) //x는 root, node
if x = NULL //못한다
then return NULL;
if k = x->key //x가 가지고 있는 data field
then return x;
else if k < x->key
then return search(x->left, k);
else return search(x->right, k);이진 탐색 트리에서의 탐색&삽입&삭제 연산의 시간 복잡도는 트리의 높이를 h라고 했을 때 h에 비례한다.
최선의 경우(이진 트리가 균형적으로 생성되어 있는 경우) : h = log2n
최악의 경우(한쪽으로 치우친 경사 이진 트리의 경우) : h = n, 순차 탐색과 시간복잡도가 같다.
BST의 inorder traversal는 sorted list를 생성할 수 있다.
Searching
//Searching a BST
tree_ptr search(tree_ptr root, int key){
/*
return a pointer to the node that contains key. If there is no such node, return NULL
*/
if(!root) return NULL;
if(key == root->data) return root;
if(key < root->data)
return search(root->left_child, key);
return search(root->right_child, key);
}
//iterative search of a BST
tree_ptr iter_search(tree_ptr tree, int key){
while(tree){
if(key == tree->data) return tree;
if(key < tree->data)
tree = tree->left_child;
else
tree = tree->right_child;
}
return NULL; //Null을 만날 때까지
}시간복잡도에서 평균은 O(h), h는 BST의 height. 최악은 O(n),(skewed binary tree).
Inserting
//Inserting into a BST
void insert_node(tree_ptr *node, int num){ //*node는 root node
tree_ptr ptr, temp = modified_search(*node, num)
if(temp || !(*node)){
ptr = (tree_ptr)malloc(sizeof(node));
if(IS_FULL(ptr)){
fprintf(stderr, "The memory is full\n");
exit(1);
}
ptr->data = num;
ptr->left_child = ptr->right_child = NULL;
if(*node)
if(num < temp->data)
temp->left_child = ptr;
else
temp->right_child = ptr;
else *node = ptr; //비어있는 tree면 *ptr이 루트가 됨
}
}Modified_search
NULL을 리턴하는 경우) tree가 비었거나 num이 이미 존재한다.
그렇지 않다면, last node의 pointer를 리턴한다. >> 삽입의 시간 복잡도는 O(h),h는 tree의 height
Deleting from a BST
1 child 인 경우, 트리가 끊어지지 않게 위로 올려줄 수 있다.
2 children 인 경우, 매꿔줘야하기 때문에, 좌측 우측 서브 트리를 탐색해서 좌측에서는 max, 우측에서는 min을 골라 그 자리를 대체하도록 한다. 그걸 반복해서 완성하도록 한다. 이때, 좌측 서브 트리의 max는 leaf node 거나 1 child 상황이 된다.
Height of a BST
BST가 n개의 element를 가지고 있을 때의 height는, 평균 케이스는 O(log2n). 최악 케이스일 때는 O(n), 초기상태의 빈 BST에서 1부터 n까지의 node를 삽입한 경우이다.
Balanced search tree
최악의 경우 height는 O(log2n)이다. searching, insertion, deletionn은 O(h), h는 binary tree의 height이다. 균형잡힌 탐색 트리는 AVL tree, 2-3 tree, red-black tree 이다.
Forest
forest란 n개의 disjoint tree의 집합이다. 트리에서 루트를 제거하면 포레스트가 된다.
forest를 binary tree로 변환하는 방법 : 1. forest에 있는 각 트리를 이진트리로 변환한다. 2. 변환된 모든 binary tree를 root node의 right child 필드를 통해 연결한다.
preorder traversal
//forest traversal
//preorder traversal
1. if F is empty, then return
2. visit the root of the first tree of F
3. traverse the subtrees of the first tree in tree preorder
4. traverse the remaining trees of F in preorder
>> binary tree에서의 preorder와 동일 |
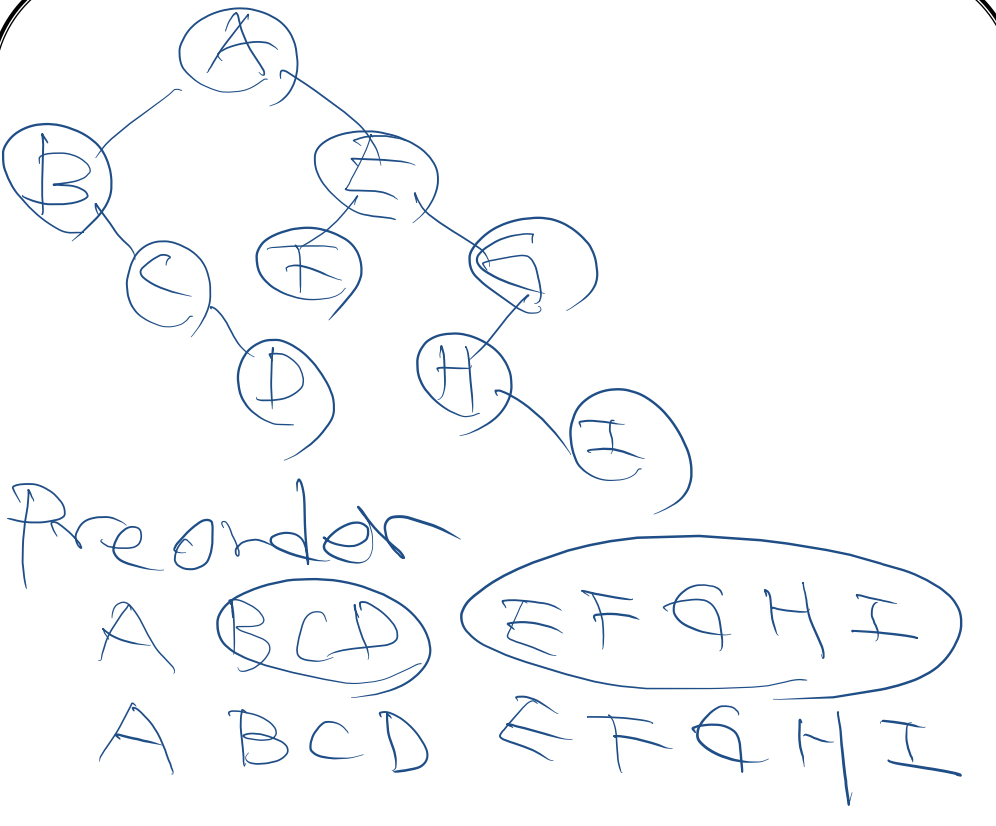 |
inorder traversal
//forest traversal
//inorder traversal
1. if F is empty, then return
2. traverse the subtrees of the first tree in tree inorder
3. visit the root of the first tree of F
4. traverse the remaining trees of F in inorder
>> binary tree에서의 preorder와 동일 |
 |
post traversal
//forest traversal
//postorder traversal
1. if F is empty, then return
2. traverse the subtrees of the first tree in tree postorder
3. traverse the remaining trees of F in postorder
4. visit the root of the first tree of F
>> binary tree에서의 preorder와 다르다고 하나 결과는 같게 나왔음 >> counting example 발견하기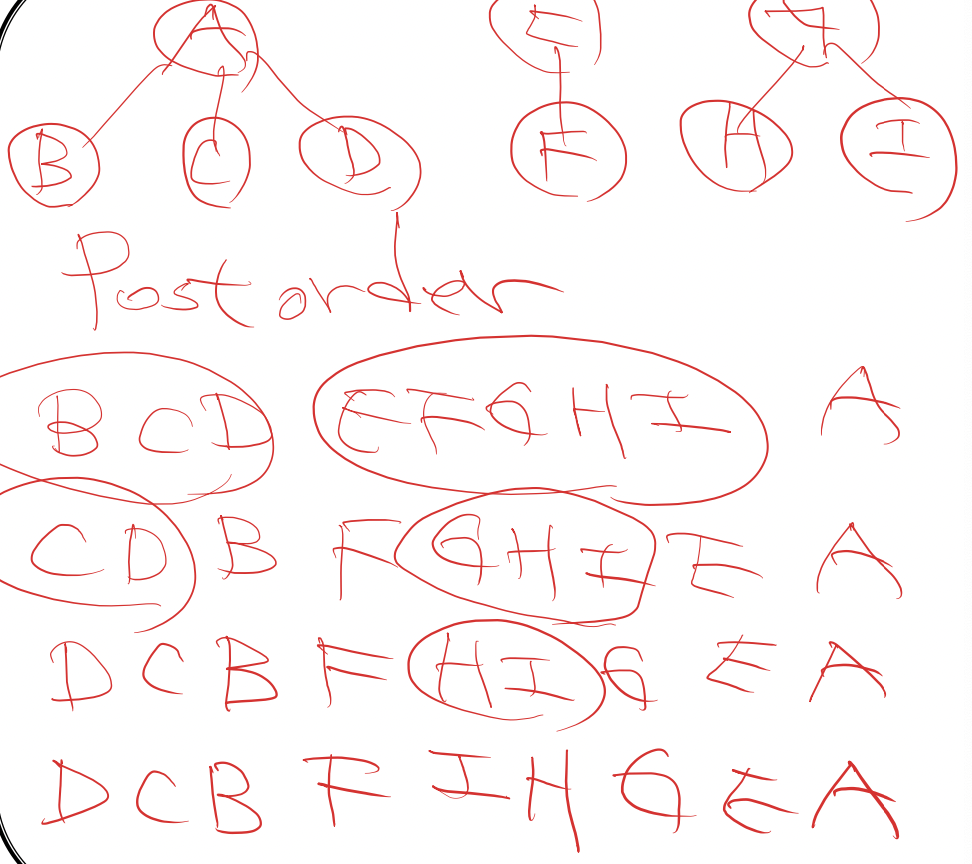 |
 |
Set Representation
집합을 트리를 이용해서 어떻게 표현할 수 있을까? >> disjoint set union // find
두 개의 원소가 같은 집합에 있는지 확인하기 위해, 루트 노드의 원소를 대표 원소로 볼 수 있음 >> 집합명은 중요하지 않다.
집합을 트리로 표현하는 방법 > 트리를 array로 표현
int find1(int i){
for(; parent[i] >= 0; i = parent[i]);
return i;
}
void union1(int i, int j){
parent[i] = j; /* or parent[j] = i; */
}트리의 개수가 n일 때, find 연산은 n번 하게 되기 때문에 depth값인 n은 짧을 수록 좋다. >> 시간복잡도는 O(n^2)이다.
degenerate tree가 안 생기도록 하기 위해, adjust과정이 필요하다 >> 하나하나 연결
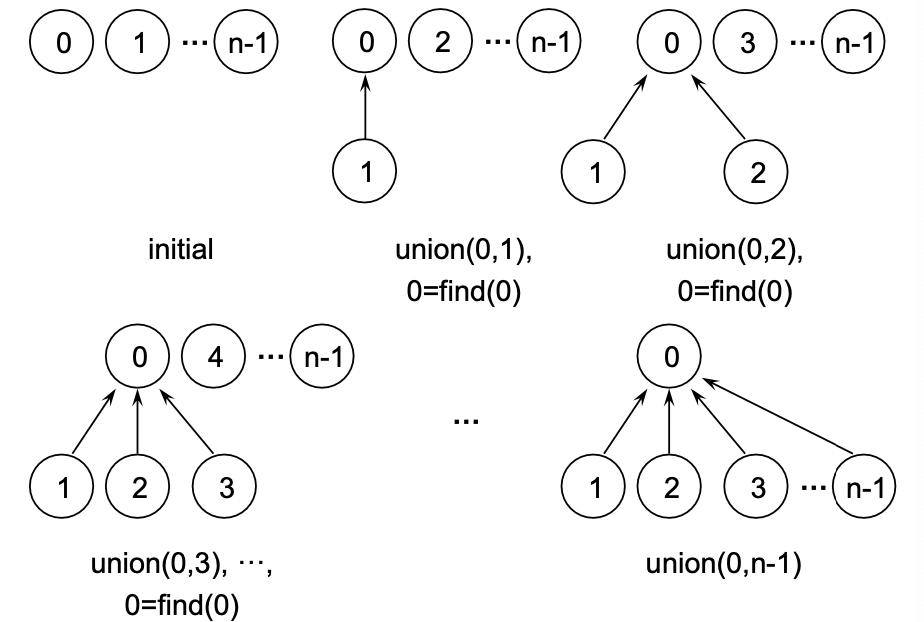
//union function
void union2(int i, int j){
/* union the sets with roots i and j, i != j using the weighting rule.
parent[i] = -count[i] and parent[j] = -count[j]*/
int temp;
temp = parent[i] + parent[j];
if(parent[i] > parent[j]){
parent[i] = j; //make j the new root
parent[j] = temp;
}
else{
parent[j] = i; //make i the new root
parent[i] = temp;
}
}
void find2(int i){
/* find the root of the tree containing element i. use the collapsing rule to collapse all nodes from i to root */
int root, trail, lead;
for(root = i;parent[root] >= 0; root = parent[root]);
for(trail = i; trail != root; trail = lead){
lead = parent[trail];
parent[trail] = root;
}
return root;
}set representation에서, n개의 요소 트리에서 시간복잡도는 O(log2n), n-1 union과 m find operation에서의 시간복잡도는 O(n + mlog2n)이다.
weighing rule : union할 때, tree i와 j 노드를 비교해 j가 더 크면 i의 부모를 j로 만드는 방법
union은 O(n), find는 O(n)
'lecture > data structure' 카테고리의 다른 글
| [lecture] BASIC CONCEPTS (1) | 2023.01.09 |
|---|---|
| [lecture] 그래프 (0) | 2023.01.09 |
| [lecture] 큐 (0) | 2023.01.09 |
| [lecture] 스택 (0) | 2023.01.01 |
| [lecture] 연결 자료구조 (0) | 2022.12.30 |




