happy coding
[lecture] 그래프 본문
그래프
그래프(graph)란 연결되어 있는 객체간의 관계를 표현하는 자료 구조이다. 예시로는, 전기회로, 프로젝트 관리 그리고 지도에서 도시들의 연결 등이 있다. 그래프 이론(graph theory)은 그래프를 문제 해결의 도구로 이용하는 연구 분야를 의미한다.
트리 또한 그래프의 일종, 트리는 acyclic graph(사이클이 없는 그래프)이다.
그래프는 오일러에 의해 창안되었으며, 여기서 오일러 문제란 "모든 다리를 한 번만 건너서 처음 출발했던 장소로 돌아오는 문제" 이다. 문제의 핵심만을 표현하기 위해, 위치는 정점으로 다리는 간선으로 표기하였으며, 정점에 연결된 간선의 개수가 짝수이면 오일러 경로가 존재한다고 할 수 있다.
그래프는 V(정점(vertices)들의 집합)과 E(간선(edge)들의 집합)로 표시된다. 따라서 정점과 간선은 모두 관련되는 데이터를 가질 수 있다. 여기서 데이터를 weight라고 한다.
그래프의 종류(방향성 유무)
| 무방향 간선 | 간선을 통해서 양방향으로 갈 수 있음, (A,B) | (A,B) = (B,A) |
| 방향 간선 | 방향성이 존재하는 간선으로, 한 쪽 방향으로만 갈 수 있음, <A,B> | <A,B> = /=<B,A> |
가중치 그래프(weighted graph), 네트워크(network) 란 간선에 weight나 가중치가 할당된 그래프이다.

인접 정점(adjacent vertex) : 간선에 의해 연결된 정점, adjacent to(from) for direct graph >> vertex와 vertex 간.
차수(degree) : 그 정점에 연결된 다른 정점의 개수
경로(path) : 정점을 나열로 표현 > 단순 경로( 0 1 2 3 ), 사이클(cycle)( first and last vertices are the same )
경로의 길이 : 경로를 구성하는데 사용된 간선의 수
완전 그래프 : 모든 정점이 연결되어 있는 그래프, 자신을 제외하고 모든 vertex간에 edge가 존재하는 그래프 >> n개의 vertice라면 n(n-1)/2가 max number of edges
incident : vertex와 edge 간
connected component(of an undirected graph) : maximal connected subgraph
strongly connected(in a directed graph) : 유향 그래프에서 모든 정점이 다른 모든 정점들에 대하여 방문할 수 있는 경우
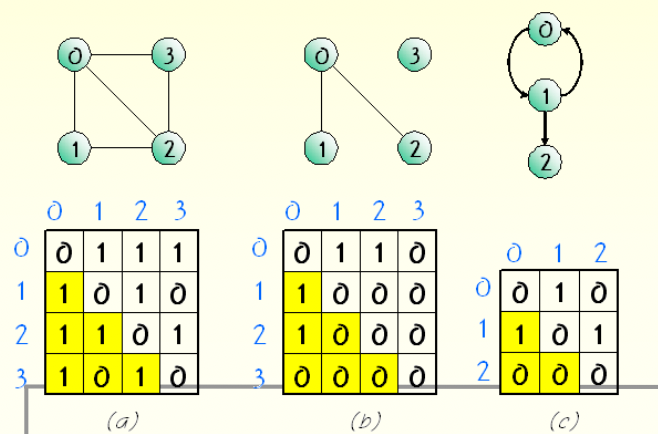
그래프를 표현하는 방법에는 1. 인접행렬(adjacent matrix) 2. 인접리스트(adjacency list) 이 있다.
| 인접 행렬 Adjacency matrix |
2차원 배열 사용 표현 | if(간선(i,j)가 그래프에 존재) M[i][j] = 1, 그렇지 않으면 M[i][j] = 0. (a)와 (b) 그래프 처럼, undirected면 대칭성이 유지되는데, (c)처럼 directed인 경우 대칭성이 유지 되지 않는다. graph 일때는 matrix로 표현하는 게 더 효과적이다. |
 |
| 인접 리스트 Adjacency lists |
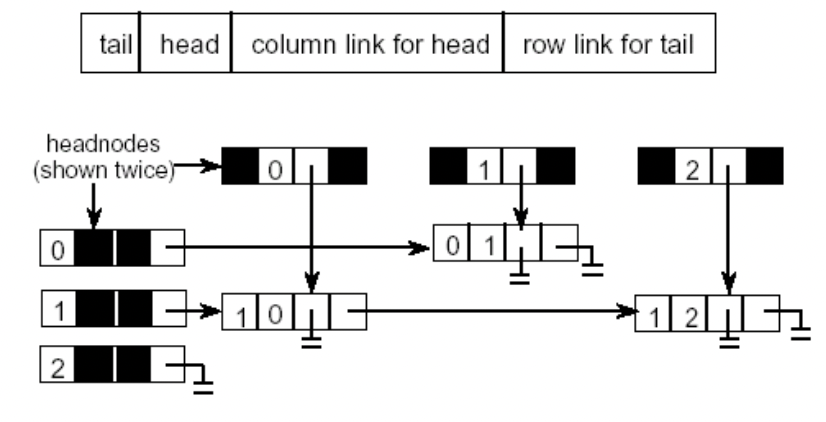
연결리스트를 사용 표현 | 각 정점에 인접한 정점들을 연결리스트로 표현, 순서는 상관없고 노드0에서는 1, 2, 3으로 갈 수 있다. 를 표현한 것이 첫 그림 첫 줄이다. Inverse adjacency lists : in-degree 찾기에 유용 각 vertex마다 하나의 list 포함, 각 lisdt는 각 vertex에 대한 node를 포함 |
 |
orthogonal representation
인접리스트의 노드 구조를 바꿈
weighted edges
- 그래프의 간선의 weight를 확인 : 1. 정점끼리의 거리 2. 하나의 정점에서 다른 인접한 정접까지 가는 데 드는 비용
- 가장자리의 무게로 가장자리를 나타내도록 표현을 수정 >> for adj matrix : weight instead of 1, for adj list : weight field
그래프 탐색은 그래프의 가장 기본적인 연산이다. 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문한다. 많은 문제들이 단순히 그래프의 노드를 탐색하는 것으로 해결한다.
| 깊이 우선 탐색(DFS : Depth-First Search) | 미로를 탐색할 때 한 방향으로 갈 수 있을 때 까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이 곳으로 다른 방향으로 다시 탐색을 진행하는 방법과 유사 stack을 이용해서 탐색한다(방문했다는 것을 표시하기 위해). recurrsive 알고리즘을 이용하면 stack을 이용하지 않아도 된다. |
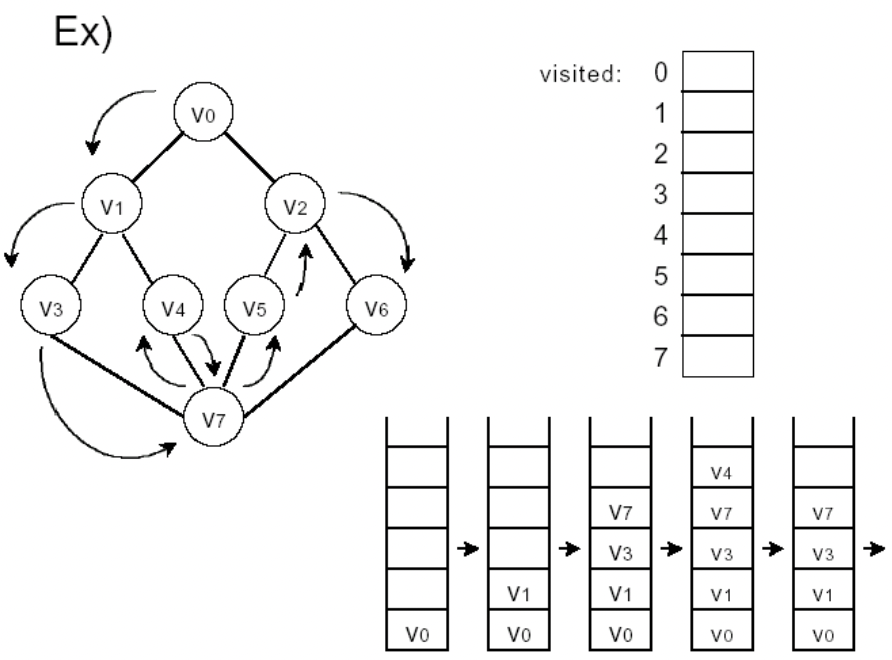 |
| 너비 우선 탐색(BFS : Breadth-First Search) | dynamic linked Queue를 이용해서 탐색한다. | 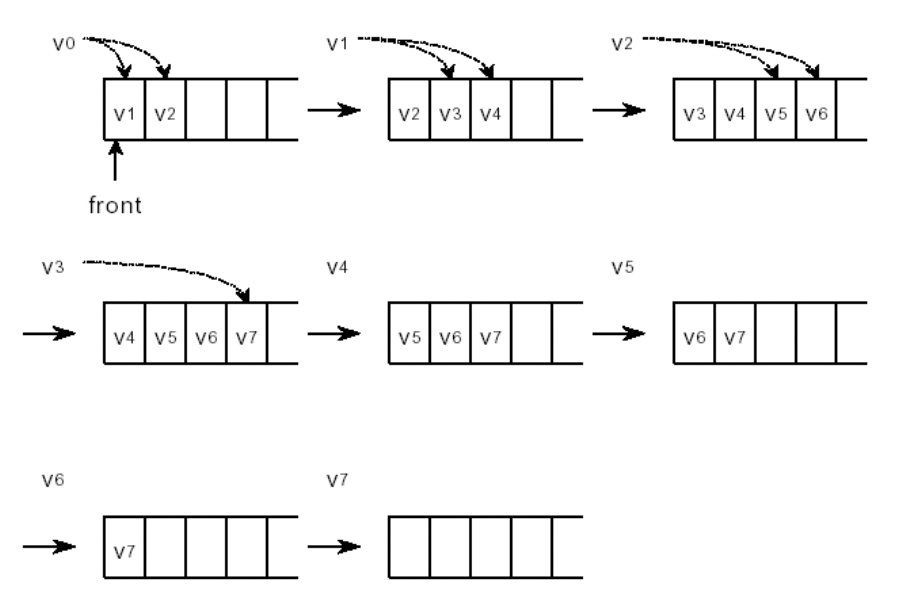 |
//depth first search
void dfs(int v){
/* depth first search of a graph beginning with vertex v */
node_ptr w;
visited[v] = TRUE;
printf("%5d", v);
for(w = graph[v]; w; w = w->link)
if(!visited[w->vertex])
dfs(w->vertex);
}
//breath first search
void bfs(int v){ //start vertex
node_ptr w; queue_ptr front, rear;
front = rear = NULL;/* initialize queue*/
printf("%5d", v);
visited[v] = TRUE;
insert(&front, &rear, v);
while(front){
v = delete(&front);
for(w = graph[v]; w; w = w->link)
if(!visited[w->vertex]){
printf("%5d",w->vertex);
add(&front, &rear, w->vertex);
visited[w->vertex] = TRUE;
}
}
}[dfs]인접 리스트의 시간복잡도는 O(e), 인접 배열의 시간복잡도는 O(n2) >> 인접 리스트를 인접 배열로 바꾸는 방법 생각
[bfs]인접 리스트의 시간복잡도는 O(e), 인접 배열의 시간복잡도는 O(n2)
connected components
- 방향이 지정되지 않은 그래프의 연결 여부 확인 >> dfs(0), bfs(0)
- 그래프의 연결된 성분을 나열 >>
//connected componenets
void connected(void){
/* determine the connected components of a graph */
int i;
for(i=1;i<n;i++)
if(!visited[i]){
dfs(i);
printf("\n");
}
}시간복잡도는 O(n+e) >> O(e)(dfs에 의한 전체 시간) + O(n)(루프)
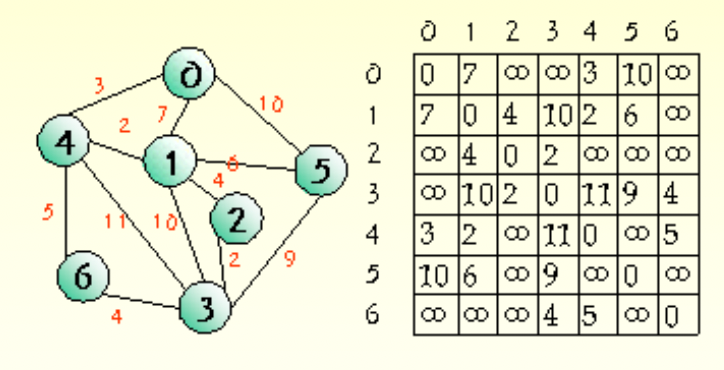
최단 경로 알고리즘(shortest path) 문제는 네트워크에서 정점 i와 정점 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제이다. 간선의 가중치는 비용, 거리, 시간 등을 나타낸다. > 네비게이션 최단 경로, 네트워크 라우팅
spanning tree
스패닝 트리(spanning tree)는 그래프 G에 있는 1. 모든 정점을 포함하고 2. 정점 간 서로 연결이 되는 (사이클 없는 >> 트리) 그래프, 그래프 G가 연결되었을 때 dfs 또는 bfs는 G의 가장자리를 두 집합(T : tree edges, N : nontree edges)으로 분할, edge 는 |v| - 1 개의 tree 형태의 subgraph
모든 정점이 포함되어 있으면서, 모든 노드는 적어도 하나의 간선으로 연결되어 있고, 연결 관계에서 사이클을 형성하지 않는다. >> 신장 트리의 정점의 개수가 n개일 때, 간선이 n-1개

bfs(0)는 T가 enqueue에 관여한 edges의 집합

Minimum cost Spanning trees(MST, 최소 신장 트리)
undirected graph에 weighted(그 전까지는 가중치를 1로 간주)일 때, 가중치(cost)의 합이 minimum이 되는 spanning tree
예시로, a spanning tree of least cost, Kruskal's and Prim's algo., greedy method
greedy method : construct an optimal solution in stages, make the best decision at each stage using some criterion >> use only edges within the graph, use exactly n-1 edges, may not use edges that would produce a cycle
dynamic programming 과 greedy method가 존재하는데, dynamic programming은 여기서 다루지 않음
그래프 내의 모든 정점들을 가장 적은 비용으로 연결하기 위해 >> 간선의 가중치의 합이 최소가 되는 상황을 구하고 싶을 때 (최소 신장 트리를 구하고 싶을 때) 사용한다.
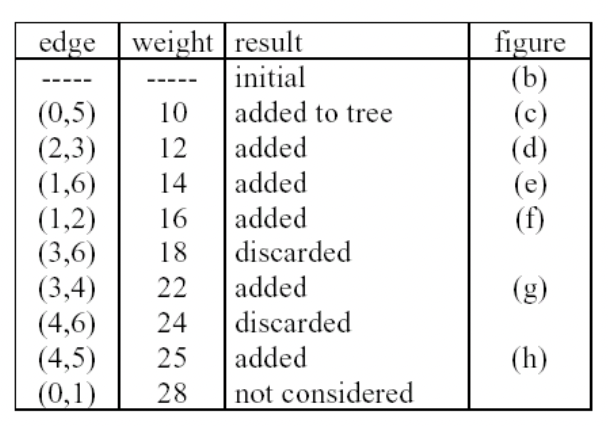
kruskal's algorithm (greedy algo의 일종)
1. 간선들을 가중치의 오름차순으로 정렬해 놓고 2. 사이클을 형성하지 않는 선에서 정렬된 순서대로 간선을 선택 3. 선택된 간선의 개수가 정점의 개수 - 1 이 되면 종료
cycle을 판단할 때, union-find 자료구조 사용한다.
union-find란, Disjoint Set(서로소 집합)을 표현하는 자료구조이고, 서로 다른 두 집합을 병합하는 union 연산, 집합 원소가 어떤 집합에 속해있는지 찾는 find 연산을 지원한다.
서로 부모가 같을 때는 union 연산을 하지 않기 때문에, 사이클을 형성하는지 알아보기 위해서는 각 노드의 부모 노드가 동일한지 아닌지 본다.
//Kruskal's algorithm
T = {};
while(T contains less than n-1 edges && E is not empty){ //min heap
choose a least cost edge (v,w) from E;
delete (v,w) from E;
if((v,w) does not create a cycle in T)
add (v,w) to T;
else
discard (v,w);
}
if(T contains fewer than n-1 edges)
printf("no spanning tree\n"); |
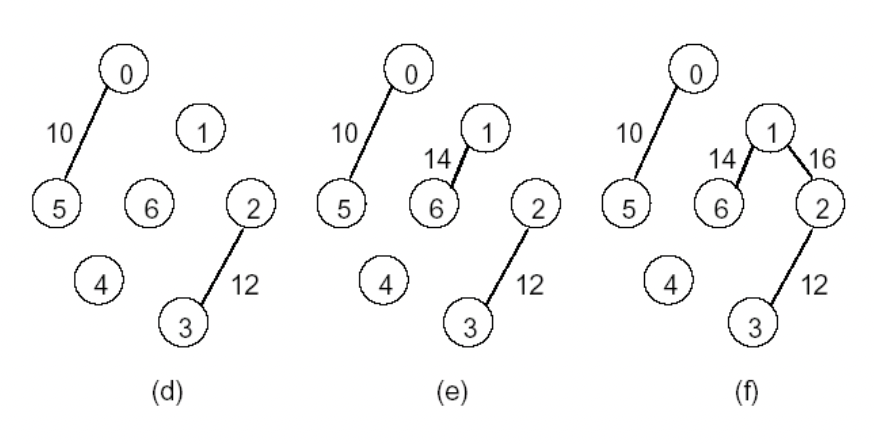 |
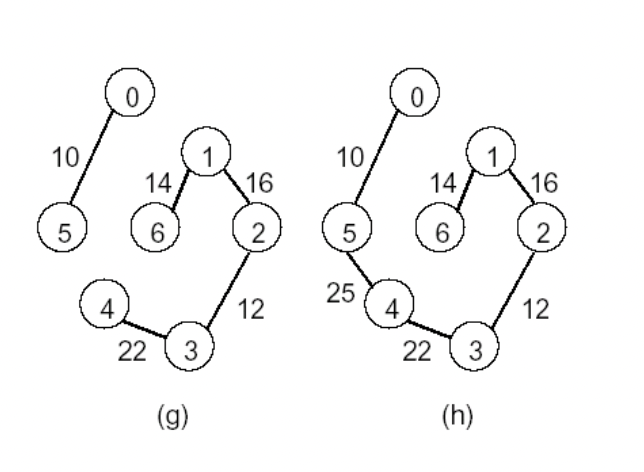 |
weight가 가장 작은 것을 넣어두고, 그다음 가중치가 작은 것을 사이클을 형성하지 않는 선에서 순서대로 넣는다.
min heap 을 이용해서 작은 것을 뽑아내는 데, 이러면 O(log2e) 발생, 총 O(e) 발생
새로운 edge를 T에 삽입하였을 때 사이클이 생성되는지 체크하는 것은 "union-find operation"을 이용한다.
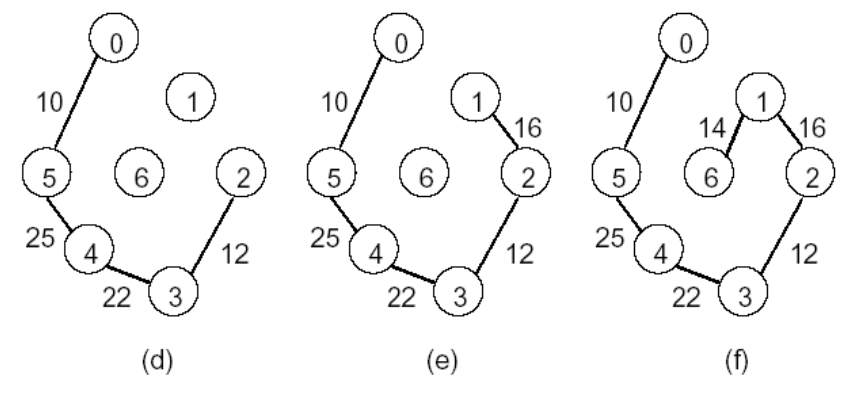
prim's algorithm
트리를 계속 확장해가면서, 최종 트리를 만드는 알고리즘, 크루스칼 알고리즘이 트리에서 포레스트를 만드는 알고리즘이라는 데에서 다름을 알 수 있다. vertex가 1개인 트리에서 시작해서, 가장 작은 비용을 가진 edge를 트리에 추가해 확장시킨다. n-1 개의 edge가 생성될 때까지 진행한다.
//Prim's algorithm
T = {}; //spanning tree에 들어갈 edges
TV = {0}; /* start with vertex 0 and no edge */ //...vertices
while (T contains fewer than n-1 edges){
let(u,v) be a least cost edge such that u ∈ TV and v ∈/ TV;
if(there is no such edge)
break;
add v to TV;
add (u,v) to T;
}
if(T contains fewer than n-1 edges)
printf("no spanning tree\n"); |
 |
shortest path
(Dijkstra) path위 edge들의 가중치의 합
single source all destinations
 |
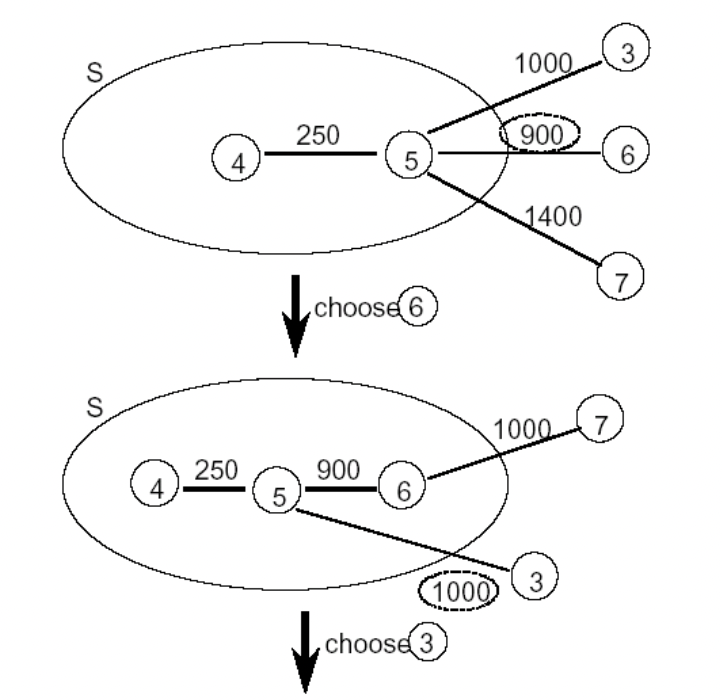
v0 : 출발 정점 S : 지름길을 이미 찾아낸 집합 W : S에 포함되지 않는 모든 집합 distance [w] : 출발점에서 시작해서 계산한 거리(지름길이 아닐수도 있음) S에 들어있는 u를 경유해서 w까지의 지름길을 찾는다. u 중 가장 작은 노드를 s에 넣어서, 지름길을 찾고 더 멀리 있는 건 u를 경유해서 가도록 한다. |
min{distance[w], distance[u] + cost[u][w]} >> u를 경유해서 w로 간다는 것
//declarations for the shortest path algorithm
#define MAX_VERTICES 6
int cost[][MAX_VERTICES] =
{{0,50,10,1000,45,1000},
{1000,0,15,1000,10,1000},
{20,1000,0,15,1000,1000},
{1000,20,1000,0,35,1000},
{1000,1000,30,1000,0,1000},
{1000,1000,1000,3,1000,0}};
int distance[MAX_VERTICES];
short int found[MAX_VERTICES];
int n = MAX_VERTICES;
void shortestpath(int v, int cost[][MAX_VERTICES], int distance[], int n, short int found[]){
int i,u,w;
for(i=0;i<n;i++){
found[i] = FALSE;
distance[i] = cost[v][i];
}
found[v] = TRUE;
distance[v] = 0;
for(i=0;i<n-2;i++){ //나머지 노드들에 대해서
u = choose(distance, n, found); //distance 중 가장 작은 것을 찾기
found[u] = TRUE;
for(w=0;w<n;w++)
if(!found[w])
if(distance[u] + cost[u][w] < distance[w])
distance[w] = distance[u] + cost[u][w];
}
}
int choose(int distance[], int n, int found[]){
/* find smallest distance not yet checked */
int i, min, minpos;
min = INT_MAX;
minpos = -1;
for(i=0;i<n;i++)
if(distance[i]<min && !found[i]){
min = distance[i];
minpos = i;
}
return minpos;
} |
 |
 |
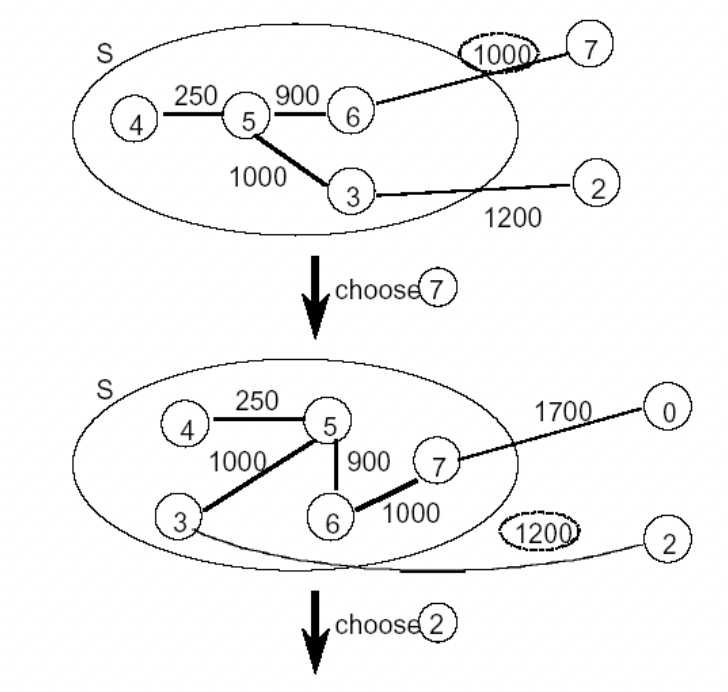 |
 빈공간은 거리가 무한대이다. |
 새로운 u가 들어올 때마다 distance 값이 업데이트된다. 하지만 원래 있던 값이 더 작은 경우 업데이트하지 않는다. 이미 업데이트한 경우 업데이트를 다시 하지 않는다. |
all pairs shortest paths
모든 쌍 최단 경로 문제는 각 쌍의 점 사이의 최단 경로를 찾는 문제이다. 이 문제를 해결하려면, 각 점을 시작점으로 시간 복잡도가 O(n^3)인 다익스트라 알고리즘을 수행하면 되는데, O(n^3)의 시간복잡도를 가지지만 더 간단한 플로이드-워셜 알고리즘 또한 수행할 수 있다.
vertex 마다 이름을 붙이고, 아무것도 경유하지 않는 vertex를 구한다음, v1.. v2..등 하나씩 늘려나가면서 경유한 것이 만약 더 작다면 업데이트한다. >> Dijk = 점 {1,2,…,k}만을 경유하는 점들로 고려, 점 i로부터 점 j까지의 모든 경로 중에서 가장 짧은 경로의 거리
(단, 점 1에서 k까지의 모든 점들을 반드시 경유하는 경로를 의미하는 것은 아님)
level order, bfs spanning tree, dfs spanning tree
shortest path > single source all distination
'lecture > data structure' 카테고리의 다른 글
| [lecture] Heap (0) | 2023.01.10 |
|---|---|
| [lecture] BASIC CONCEPTS (1) | 2023.01.09 |
| [lecture] 트리 (0) | 2023.01.09 |
| [lecture] 큐 (0) | 2023.01.09 |
| [lecture] 스택 (0) | 2023.01.01 |




