[lecture] 5주차.동적 계획 알고리즘_모든쌍 최단 경로 문제(플로이드 알고

수업을 듣고 정리한 내용입니다.

Dynamic programming(DP) : 이미 문제가 분할되어 있는 상태로, 입력 크기가 작은 문제들을 해결하기 위해 그 해를 이용해 보다 큰 크기의 부분 문제를 해결하고 최종적으로 원래 주어진 입력의 문제를 해결하는 것이 목표이다.

DP vs. 분할

동적 계획	분할
여러 layer를 취합하여 해결한다.	이전 layer를 취합하여 해결한다.

동적 계획 알고리즘은 부분 문제 사이의 의존적 관계가 존재한다. 이는 문제와 입력에 따라 다르고 대부분 뚜렷하다는 함축적 순서를 가지고 있다고 말할 수 있다. 부분 문제의 해는 중복 사용하지 않는다.

• 최적 부분 구조/ 최적성 원칙 : 문제의 최적해 중 부분문제의 최적해
• 부분문제들 사이의 관계를 빠짐없이 고려해야 한다.

모든 쌍 최단 경로 문제 (All Pairs Shortest Paths)

모든쌍 최단 경로 문제는 각 쌍의 점 사이의 최단 경로를 찾는 문제이다.  이 문제는 다익스트라 알고리즘 또는 플로이드-워셜 알고리즘을 통해 해결할 수 있는데, 다익스트라는 각 점을 시작점으로 하는 알고리즘이며, 이 때의 시간복잡도는(n-1)*O(n^2) = O(n^3)이다. 

플로이드-워샬 알고리즘(플로이드 알고리즘) 은 그래프의 모든 정점 쌍의 최단 거리를 저장하는 배열 dist[][]를 계산한다.(동적 계획법)
이 배열의 원소 dist[u][v]는 정점 u에서 v로 가는 최단 거리를 나타낸다.

아이디어

모든 점을 경유가능한 점들로 고려하고, 모든 쌍의 최단 경로의 거리를 계산한다

부분문제 찾기

그래프에 3개의 점이 있는 경우에, 점i에서 점 j까지의 최단 경로를 찾으려면 2가지 경로(j로 직접가기, 1을 경유하기)중에서 짧은 것을 선택하게 된다.

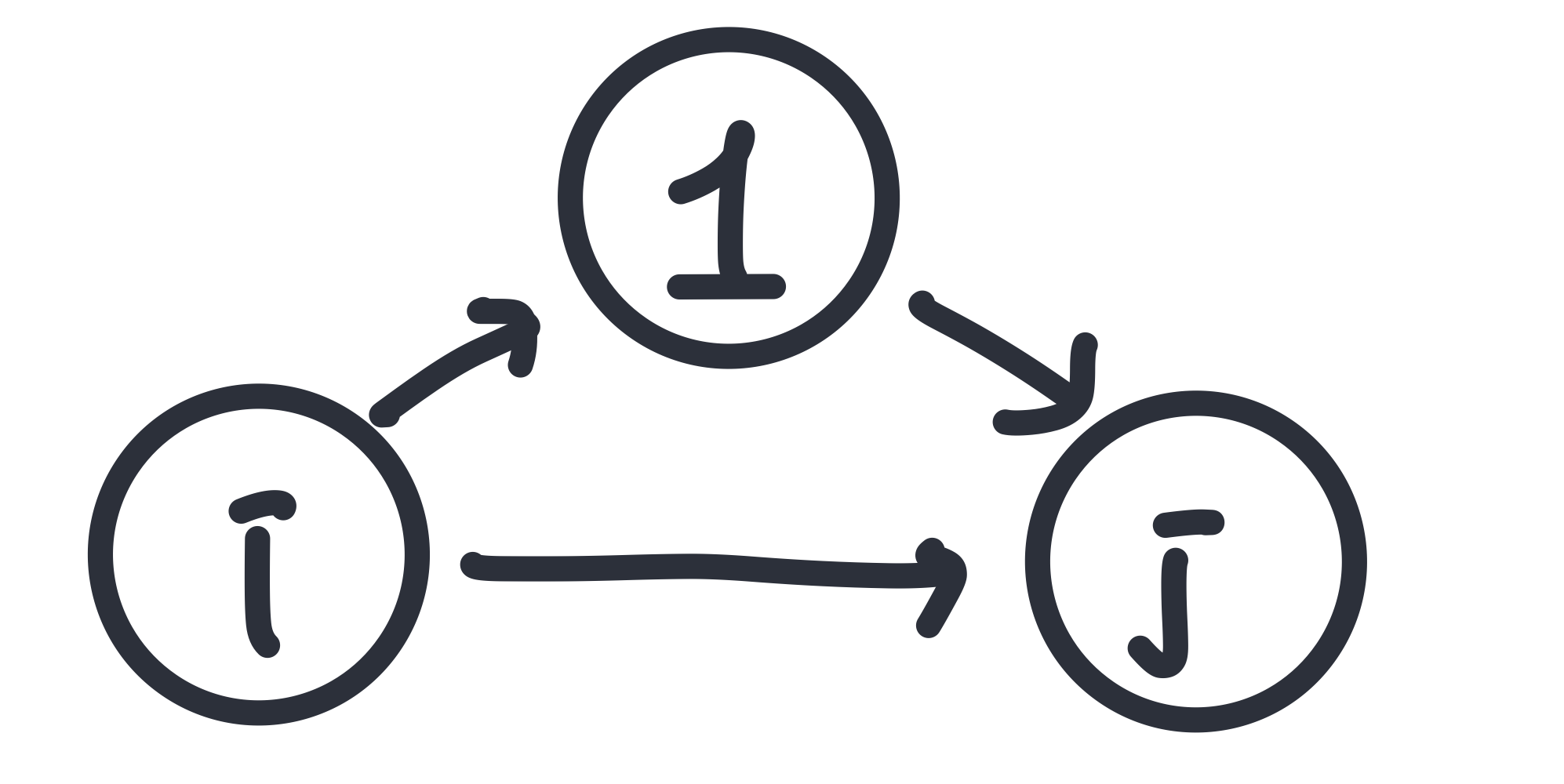
D_ij^k = 점 {1,2,…,k}만을 경유하는 점들로 고려하고, 점 i로부터 점 j까지의 모든 경로 중에서 가장 짧은 경로의 거리이다. 단, 점 1에서 k까지의 모든 점들을 반드시 경유하는 경로를 의미하는 것은 아니다.

---

예시)

• D_ij^1은 i에서 점 1을 경유하여 j로 가는 경로, i에서 j로 직접 가는 경로, 즉 선분 (i,j) 중에서 짧은 거리이다. 단, i≠1, j≠1
• i에서 점 2를 경유하여 j로 가는 경로의 거리와 D_ij^1 중에서 짧은 거리를 D_ij^2로 정한다. 단, 점 2를 경유하는 경로의 거리는 D_i2^1 + D_2j^1 이다. 단, i≠2, j≠2
• i에서 점 k를 경유하여 j로 가는 경로의 거리와 D_ij^k-1 중에서 짧은 것을 D_ij^k로 정한다. 단, 점 k를 경유하는 경로의 거리는 D_ik^(k-1)+D_kj^(k-1)이다. 단, i≠k, j≠k

이런 방식으로 k가 1에서 n이 될 때까지 D_ij^k를 계산하여 모든 점을 경유 가능한 점들로 고려된 모든 쌍 i와 j의 최단 경로의 거리를 찾는 방식이 플로이드의 모든 쌍 최단경로 알고리즘이다.

시간 복잡도

각 k에 대해 모든 i,j 쌍에 대해 계산하는데 이것은 n*n*n으로 표현된다. 그리고 각 계산은 O(1)을 소요하기 때문에 시간 복잡도는 O(n^3)이다.

pseudocode

input : 2차원 배열 D, 단 D[ij] = 간선 (i,j)의 가중치, 만일 간선 (i,j)가 없다면 D[i,j]값은 무한대이다. 모든 i에 대해 D[i,j] = 0
output : 모든 쌍 최단 경로의 거리를 저장한 2차원 배열 D

AllPairsShortest
for k = 1 to n
	for i = 1 to n ( i =/= k)
    	for j = 1 to n (j =/= k, j =/= i)
        	D[i,j] = min{D[i,k] + D[k,j], D[i,j]}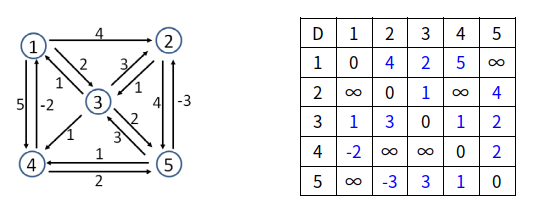

배열 D의 원소들이 k가 1부터 5까지 증가함에 따라서 갱신된다. 표에서 세로축은 출발점, 가로축은 도착점이다.

---

계산 다시 해보기 이해가 안감

https://nolzaheo.tistory.com/10